К выводу преобразования Лоренца

Как известно [1], специальная теория относительности базируется на принципе постоянства скорости света и принципе относительности, который заключается в неизменности законов природы от выбора инерциальной системы отсчета (ИСО). Рассмотрение двух таких систем, движущихся друг относительно друга, приводит к понятию интервала, из инвариантности которого по отношению поворотам в пространстве Минковского получаются преобразования Лоренца. Ниже приводится вывод этих преобразований с помощью введения специального поворота в обычном пространстве без использования принципа относительности, а также обсуждение этого результата.

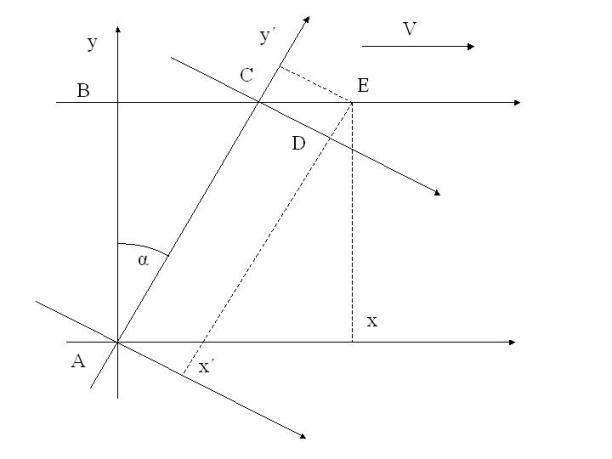
Вначале, как обычно, мы введем в рассмотрение две ИСО: K – считающаяся неподвижной и K’ – движущаяся со скоростью V. Пусть оси координат обоих систем параллельны и скорость V направлена вдоль оси x (см. рис.1). Представим, что в начале системы отсчета K находится один наблюдатель, а в системе K’ на некотором расстоянии мимо него движется другой наблюдатель. Допустим, что в начальный момент времени наблюдатели будут находиться на кратчайшем расстоянии друг от друга в направлении, например, оси y.

Рис.1

Далее рассмотрим два события, заключающиеся в излучении импульсов света из обеих систем отсчета, а именно: из точки A, где находится неподвижный наблюдатель, и точки B, где будет находиться движущийся наблюдатель в начальный момент времени своего движения. В этом случае легко сравнить времена, за которые наблюдатели смогут увидеть «чужие» вспышки. Каждому наблюдателю в соответствии с принципами теории относительности должно казаться, что эти вспышки дойдут до них быстрее, чем «свои».

Действительно, из отражающего точку зрения неподвижного наблюдателя построения на рис.1 видно, что отрезок пути, пройденный светом, AC при движении системы K’ больше отрезка AB или, точнее,

ct ‘= ct cos µ ,. (1)

где с – скорость распространения света, µ - угол CAB, t обозначает время, за которое распространится свет в системе K от точки A до точки C, а t’ – соответствующее время в системе K’ от точки B до точки A.Из построения также видно, что

Vt = ct sin µ (2)

Поскольку с точки зрения неподвижного наблюдателя положение источника света не совпадает с излучением от него, можно представить себе, что относительно его точки наблюдения произошел поворот: системы отсчета, в которой находится этот источник, т.е. системы K’, на угол µ . При этом повороте ось x’ не совпадает по своему направлению с осью x, но положение произвольной точки D на этой оси должно казаться неподвижному наблюдателю находящимся на «своей» оси x в виде проекции этой точки так, как это обозначено на рис.1 пунктиром, т.е. в положении точки E. Тогда связь координат запишется в виде

x = x’ / cos µ + ct’ tg µ . (3)

Точно также уравнение (1) представится в следующем виде, в котором

учтен член, вызванный этой проекцией (отрезок DE)::

ct = ct’ / cos µ + x’ tg µ . (4)

Если с помощью уравнения (3) выразить x’ через x и t’ и подставить его в (4), то можно получить следующие уравнения, формально выражающие ортогональное преобразование системы координат:

x ‘ = x cos a - ct’ sin a , (5)

ct = x sin a + ct’ cos a . (6)

Поскольку отрезок AB, равный ct’, находится на оси y, а отрезок AC, параллельный ct, - на оси y’, то оказывается вполне законным говорить о повороте системы координат, при котором координаты (x,y ) преобразуются в координаты (x’,y’) под действием единичной матрицы

æ cos a -sin a ö

è sin a cos a .ø

Выражая тригонометрические функции в уравнениях (3) и (4) через скорость V в соответствии с уравнением (2), мы получим преобразования Лоренца в стандартном виде:

x’ + Vt

x = ^___________(7)

Ö 1 – (V / c)²

t’ + Vx’ / c ²

t =^{_____________}(8)

Ö 1 – (V / c)²

Для заключения об обоснованности предложенного вывода преобразований Лоренца следует заметить, что поворот системы отсчета K’, произведенный в момент времени t, является полностью воображаемым. Действительно, ведь по условию K’ – это инерциальная система с осями параллельными осям системы K.Если бы произошел реальный поворот системы K’, то он означал такое активное преобразование системы отсчета, которое отличалось бы от простого смещения системы отсчета K’ вдоль оси x на расстояние равное Vt в момент времени t.

Поэтому, чтобы попытаться прояснить ситуацию, вернемся еще раз к интерпретации уравнения (1), которое может трактоваться как проявление замедления времени в подвижной системе отсчета.

В уравнении (1) с равным успехом мы можем отнести промежуток времени t’, приписанный первоначально системе K’, системе K, понимая под ним время, необходимое свету для прохождения расстояния от точки A до точки B вдоль оси y. Таким обрахом, мы имеем два световых луча, исходящих из точки A: один, соответствующий V = 0, до точки B и другой до точки F, отражающей координату y' движущегося объекта.

Поэтому правильней говорить о пассивном повороте осей координат в одной системе отсчета K. Такой поворот изменяет значение отдельных координат выбранного объекта, не меняя его положения. Тогда вместо роли интервала теории относительности выступает действительное расстояние до этого объекта. В данном случае это расстояние между точками A и E.

Таким образом, для того, чтобы предлагаемый вывод соотношений Лоренца оказался верным, необходимо допустить наличие специфического поворота осей координат в системе отсчета неподвижного наблюдателя, который возникает при движении тела. А именно, этот поворот осуществляется в плоскости, в которой происходит движение и находится «посторонний», т.е. не лежащий на пути движения, наблюдатель, на угол равный arcsin (V/c). Хотя мы не приводим в данной работе достаточно убедительного обоснования используемому построению, такое представление приводит к правильным преобразованиям Лоренца, при этом исключается необходимость введения другой системы отсчета, связанной с движущимся объектом .

Для более полного понимания сути вопроса, по-видимому, необходимы новые идеи, объясняющие результаты эксперимента Майкельсона-Морли, который и явился непосредственной причиной появления лоренцева сокращения. Одним из подходов к этому пониманию, на наш взгляд, может служить физическое обоснование вышеупомянутого поворота в рамках более широкого рассмотрения.

---------------------

[1] Ландау Л.Д., Лифшиц Е.М. Теория поля. М., Наука, 1973.