The reference frames in 4D-model of aether

V.Skorobogatov

It was shown [1] that the null result of the Mickelson-Morley experiment might be explained by means of existence of speeds of light both more and less then standard value c. It may depend from the velocity of mirror v, from which the light is glanced. Otherwise the discrepancy in light paths in longitudinal and transverse directions in the interferometer would be reached the second power of v/c, where v is the velocity of aether with respect to the Earth where the experiment is supposed conducted.
Here we take up the meaning of the reference frame in the model and the question about the so called time delay, that is the one of the debatable consequence of the theory of relativity.

The application of the Galilean transformation used in the discussion of the MMX result in [1] demands more grounding for its using in the form proposed.

For the beginning let us consider two reference frames in 3D space, K and K'. One of them is at rest and other is in motion with the constant velocity v. Usually the reference frames is being chosen with the corresponding axes parallel each other. Then if the velocity is directed along axis x the Galilean transformation can be put down like

x' = x - vt.

(1)

There is simple mutual relation, or symmetry, between both systems when they are changing:

x = x' + vt.

(2)

We see that only sign of v is changed while the frames is altered. Time t is not changed under this transformation.
The demand of the collineation of the axes is not strict. One may choose any orientation for the frame. For example, if the moving frame K' turned around third axis on the angle α with respect to the correspondent axis of the frame K, the relation (1) changes to the following

x' = (x - vt) cos(α).

(3)

It is needed to note that because the operations of the rotation and translation are not commute the order of these operations is important. Here the translation on the distance vt along x proceeds before the rotation.
Such transformation don't give any new meaning in the consideration of the movement unless to take into account of broken symmetry between two systems:

x = x'/ cos(α) + vt

(4)

Certainly, the difference in the forms of eqs.(3) and (4) doesn't indicate that the mutual velocity of the frames is changed. One must take into account the alteration of the second coordinate when the direction of the velocity in the system K' is changed. In general case, the eq.(3) can be writen as

r' = M (r - vt)

(5)

where M is the orthogonal matrix describing the rotation. The inverse transformation looks like that

r = M*r' + vt,

(6)

The velocity v in one frame transfers into Mv in another one turned on the angle α.
It was supposed implicitly that the both frames may be connected with the bodies. In classical physics the material point stands for the body as the best abstraction but it is not so in 4D-model of the aether. The approximation of the physical body, as well as a separate particle, is 2D-object, the string or line crossing the border. Hence the 4D reference frame ought to reconcile with position of the moving body. It was shown [1] that the body at rest with respect to the medium corresponds the line normally directed to the border of the medium and its motion means the existence of the tilt. That is why we must turn the moving reference frame if we want it to be connected with the moving body. The angle of rotation must be same as the tilt angle of the line. Then if we make a burst in the direction of movement the observer in that frame didn't notice any motion of bodies moving with him.

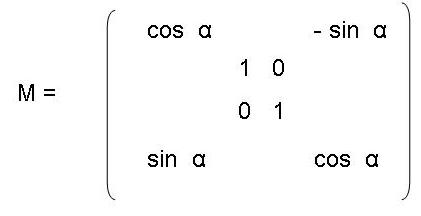
We can describe such rotation in 4D space by matrix

(7)

Here it is supposed that r is 4D radius vector. Note that the rotation in 4D space is operated not around the single axis but around two axes, or around plane pulling on these axes. Here it is the plane formed by second and third axes. Using this matrix in eq.(6) one easily get

x = x'cos(α) - z' sin(α) + vt
z = x'sin(α) + z' cos(α)

(8)

where z is the forth coordinate of the point in 4D media. Let us choose the border to be describe by expression

z = 0

(9)

Then if to extract z' from (8), we get from the first equation exactly eq.(4). Now if to take into account that in concordance with [1]

v = c sin α,

(10)

eq.(4) can be represented as

x' = (x - vt)/√(1-(v/c)²)

(11)

It is nothing more then the Lorentz transformation for the spatial coordinate.
Substituting (10) in the first eq.(8) we get

x = x'cos(α) - (z'- ct) sin(α)

(12)

It looks like the first part of the orthogonal transformation. We can construct the second part formally

z - ct' = x'sin(α) + (z'- ct) cos(α)

(13)

Then substracting it from the second eq.(8) it is easy to get the following equation

t' = t cos(α)

(14)

On the other hand, if to set

z = z' = 0

(15)

and to use the determination of the velocity by eq.(10) one get the Lorentz transformation for the time

t = (x'v/c² + t')/√(1-(v/c)²)

(16)

To get reciprocal transformation one must put this expression in eq.(11) and make some simplifications:

t' = (-xv/c² + t)/√(1-(v/c)²)

(17)

Discussion

To better imagine yourself the meaning of the expressions obtained here let us consider the Fig.1 where the situation with two reference frames such as in [1] is presented. Here coordinate axis y represents any direction in the plane formed by second and third axes. Together with axis x this plane composes the 3D space, or "world", corresponded to eq.(9). It depicted on the Fig.1 as a horizontal plane. Two planes crossing it were showed as well. They represent the positions of the moving reference frame at two moments of time, at the start moment and at the moment t. They are tilted with respect to the world in such a way that the fourth axes z' indicates to the moving body denoted by dotted line.

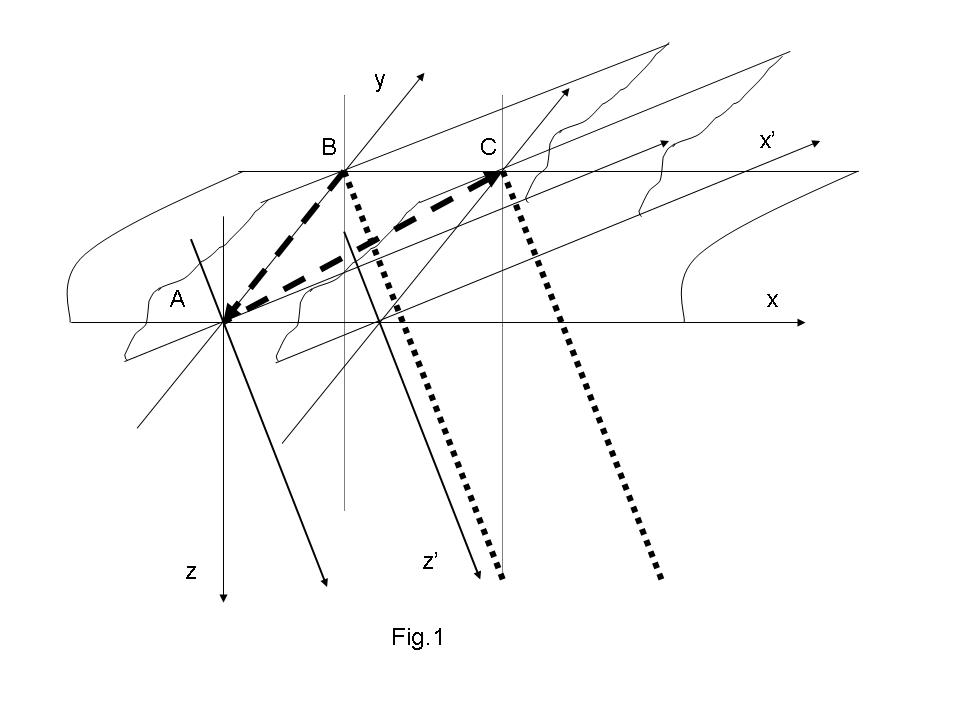Let us imagine that from the beginning of the rest frame marked by letter A as well as from the beginning of the moving frame marked by letter B simultaneously was emitted the beams of light denoted by dashed lines. Because the light can be transmitted only within world with constant velocity c it is easy to get eq.(10). The distance ct' is the path gone by light from point A to point C where the beginning of the moving frame will be. Therefore the time t' is the time needed by light in both coordinate systems. But in contrast to the rest observer at the point A the observer moving from point B to point C can not notice that the light goes behind his coordinate system. The light path AC is not contained in his reference frame as a whole. The moving observer can imagine that the light goes from moving (with respect to his place in opposite direction) observer A to B and conclude that his time (i.e. time needed to the light signal to pass distance from his place to the place where must be the other observer) is delayed. It will not be true if to consider the whole picture in four dimension. We see that the light in the moving frame goes only along the mutual crossing of the both coordinate systems, i.e. along the 2D plane normally disposed to the velocity vector. The moving observer can not perceive the light pass BA because it goes off from this plane during the motion.

Therefore we can tell about the time delay only conventionally as well as about the length contraction. The distance BC also is not containing in the moving reference frame but crossing it. From the moving frame the observer perceives the projection of the real distances belonging to the world. Formulae of the Lorentz transformation are true when the condition (15) is fulfilled. Again the latter corresponds to the plane of the mutual crossing of the both systems and can not be extended to the whole frames. Essentially, the first formula (11) is obtained from the Galilean transformation (8) for the two coordinate systems rotated with respect to each other. The second formula of the Lorentz transformation (17) also arose from the Galilean transformation but under additional proviso given by eq.(15) restricting the region of consistent space.

Another hint is contained in eqs.(12,13). Expression z - ct is looks like an argument of some wave function f. For if it is right to put down the wave equation

∂_t²f - c²∂_zf = 0

Therefore we can imagine that there are two waves moving along axes z and z' with the light speed c. The former is correspond to the body at the point A, or to the unmoving observer, and the latter to the moving body. The value z' - ct divided by the wave length is correspond to the constant phase of the wave from the point of view of the fixed observer. Relations (12,13) is about the changing of the wave phase during the motion.

It help us to describe the emission process in the following way. The wave existing in some atom inside its fourth dimension reachs the border, or the world, and make disturbance in it. Because the phase of the "inner" wave at the moment when it reachs the surface is arbitrary, the "outer" wave receives arbirary direction. The outer wave, the visible light, has the same wave length as the inner one and moving with the same velocity along the border. If it impacts on the other atom with the suitable parameters it absorbs by this atom, by atoms' electrons. It approved the statement made in [1] that the photon is a part of the electron.

The postulates of the relativity theory presuppose the parallel disposition of the both reference frames. Therefore the changing of the lengths and times occurs to accommodate with the tilt of the moving reference frame with respect to the rest one. To speak it by other words, the moving observer lives in the "imaginary world" which has only a plane perpendicular to the velocity vector as a common part with the observer at rest. His world is produced by the sliding rotation and his estimations of the lengths and times in it are wrong. It does not mean the special theory of relativity is not true. It works but don't give the real picture for the 4D model of the aether. It introduces the artificial 4D spacetime instead to give the correct result. Here it is showing how one could interpret it in the real geometrical space.

Addition. On the notions of STR.

Addition 2. The velocity transformation.

[1] V. Skorobogatov. The light in 4D model of the aether. http://vps137.narod.ru/article2a.html. 2006.