О массе в модели 4D-эфира.

Как известно из теории относительности, релятивистская масса тела зависит от скорости движения V в соответствии с формулой

	m = m₀γ,							(1)

где m₀ - масса покоя, γ = 1/√(1 - (V/c)²). Поскольку в 4D модели тело представляется одномерным объектом, струной или нитью, а его скорость связывается с углом отклонения струны от нормального положения относительно гиперповерхности [1], то представляет интерес выяснить геометрический смысл массы.

Для того, чтобы подойти к решению этой задачи достаточно предположить, что масса элементарной частицы пропорциональна длине струны L. При движении из-за наклона струна "вытягивается", как это показано на рис.1. (Здесь можно сказать и обратное: именно из-за растяжения струны происходит ее движение. Она стремится занять исходное, "вертикальное" положение.) Длина струны становится равной

	L = L₀/cos α.								(2)

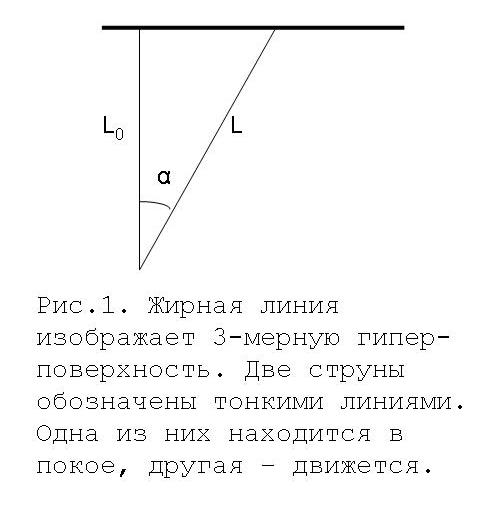Поэтому, учитывая, что sin α = V/c, можно отождествить m и L, массу частицы-струны и длину струны-частицы в дополнительном, четвертом измерении. Когда мы имеем некое тело, то его масса в силу свойства аддитивности масс складывается из суммы масс, т.е. длин, всех частиц, образующих это тело. Однако на близких расстояниях между струнами возникают взаимодействия, которые нарушают аддитивность длин и приводят к дефекту масс.

При этом отождествлении размерность массы (граммы, килограммы) заменяется на размерность длины (метры, сантиметры). Соответственно этому, можно определить остальные размерности физических величин. Размерностью, например, силы становится размерность квадрата скорости.

Для энергии струны будет существовать аналогичная зависимость от скорости V, если допустить, что вся энергия является кинетической. Тогда ее можно связать с движением среды ("эфира") вокруг и вдоль оси струны так, как это должно быть для вихря, моделью которого является струна. Естественно, кинетическая энергия струны E будет пропорциональна длине, если также предположить, что распределение абсолютной величины усредненной по поперечному сечению струны скорости движения среды равномерно вдоль оси струны. Так будет, если будет постоянным квадрат усредненной скорости среды, приходящийся на единицу длины струны. Обозначив его как c² мы приходим к знаменитому выражению

	E = mc².							(3)

Конечно, модель одномерной струны не годится для того, чтобы с ее помощью описать движение точек среды со скоростями, близкими к скорости света c. Тем более, что представить себе вихревое вращения достаточно трудно, поскольку оно в четырехмерном пространстве происходит вокруг двумерной плоскости. Более подробно мы его рассмотрим в следующих работах. Здесь мы только укажем, что внутри реального вихря вдоль ее оси должна быть пустая полость и должна существовать сила, которая уравновесит центробежные силы, с которыми среда стремится удалиться от этой полости при своем вращении. Такой силой является сила поверхностного натяжения в полости, равная σK, где K - средняя кривизна, а σ - коэффициент поверхностного (или "гиперповерхностного") натяжения. Для упрощения будем считать, что вихрь обладает симметрией четырехмерного цилиндра. Поперечным сечением его полости является сфера. Если ее радиус равен a, то для того, чтобы частицы среды, образуюшие стенки вихря, находились в равновесии, т.е. на поверхности Бернулли, необходимо достижения минимума величины

	u_s²/2 + 2σ/a. 						(4)

Здесь σ отнесена к единице массы (или к единице длины вихря), а u - скорость вращения стенок вихря, которую мы представим в виде aω, где ω - угловая скорость вращения. Находя минимум выражения (4), мы получим

	a³ = 2σ/ω².						(5)

Таким образом, размеры вихря не могут быть произвольными и связь радиуса вихря с периодом вращения T = 2π/ω имеет тот же вид, какой имеет второй закон Кеплера. Скорость стенок вихря, найденная из уравнения (5),

	u_s = aω = √(2σ/a). 				(6)

расходится при a = 0. Это и позволяет предположить, что существует минимальное значение a, которому соответствует максимальная скорость.

Чтобы вычислить кинетическую энергию вихря, необходимо знать распределение скоростей всех частиц среды во всем пространстве. Примем для абсолютной величины скорости этих частиц следующую простую зависимость в качестве такого распределения

	u = u₀ exp -a/μ.						(7)

Здесь μ - параметр затухания скорости, имеющий размерность длины, и u₀ - некая виртуальная скорость в центре полости вихря при a = 0. Реальная скорость стенок вихря u_s определится при подстановке в (6) r = a. Сравнивая два последних выражения можно найти a из следующего уравнения

	u₀ exp -a/μ = √(2σ/a).					(8)

Интегрируя половину квадрата u по всему 4-мерному пространству, мы найдем величину, которую можно назвать энергией вихря

  E = 4πμLu₀²exp -2a/μ(a² + aμ + μ²/2)							(8)

Здесь предполагается однородность распределения скорости вдоль оси вихря. Для того, чтобы избежать этого предположения, которое, очевидно, нарушается вблизи гиперповерхности, можно использовать некую эффективную длину вихря и понимать под u₀ в (7) усредненную по четвертой координате скорость. Используя (8), энергию вихря можно представить в следующем виде

  E = 8σπμL(a + μ + μ²/2a)						(9)

Варьируя по a, можно найти минимальное значение энергии

  E = 16σπa²L(1 + √2),						(10)

которое достигается при

  a = μ/√2.							(11)

Окончательно получится уравнение (3), если обозначить

	с² = 2σ/a						(12)

	m = 4πa³L(1 + √2)					(13)

Таким образом, масса пропорциональна L и имеет своим коэффициентом пропорциональности величину 4πa³(1 + √2), которая равна трехмерному объему поперечного сечения 4πa³/3, умноженному на 3(1 + √2) = 7,2426. Можно сказать, что с учетом этого числового коэффициента масса представляет собой 4-мерный объем, занимаемый полостью вихря. Однако благодаря постоянству a этот объем зависит только от L, по крайней мере не для очень больших отклонений оси вихря от нормали к гиперповерхности. В последнем случае можно ожидать иной вид зависимости (1).

Условие (13) означает, что v_s равна, как и было сказано выше, максимально возможной скорости, т.е. скорости света c, которая соответствует минимально допустимому размеру полости вихря. Вихри с большими размерами могут также существовать, но они не стабильны. На роль реальной частицы со свойствами описанного в данной работе вихря может претендовать стабильная частица, например, электрон.

Таким образом, предположение о пропорциональности массы частицы и ее длины в четвертом измерении можно считать вполне обоснованным и четырехмерная модель среды позволяет в определенной мере подойти к решению поставленной Уилером задачи сведения физики к геометрии.

[1] В.Скоробогатов. Свет в 4D-модели эфира.2006. http://vps137.narod.ru/article2.html.

exp(-1/√2) = 0,493068691