About the mass in the model of 4D-aether.

It is known from the theory of relativity that the mass m depends on the movement velocity V in accord with the formula

m = m₀γ,

(1)

where m₀ is the rest mass and γ = 1/√(1 - (V/c)²). While, as an approximation, the body in the model is represented by 1D object, by string or thread, and its velocity is coupled with the normal position deviation angle with respect to the hypersurface [1], it is rendering some interest to clarify the geometric meaning of mass.

To approach towards a solution of this task it is sufficient to suppose that the mass of the fundamental particle is proportional to the string length L. Under the movement the string "stretches" due to the slope as it is shown on the Fig.1. (Here otherwise one can say that it is namely due to the stretching of the string the latter proceeds in its motion. It behaves itself as if it eagers to be in the initial, "vertical" position.) The length of the string is equal to

L = L₀/cos α.

(2)

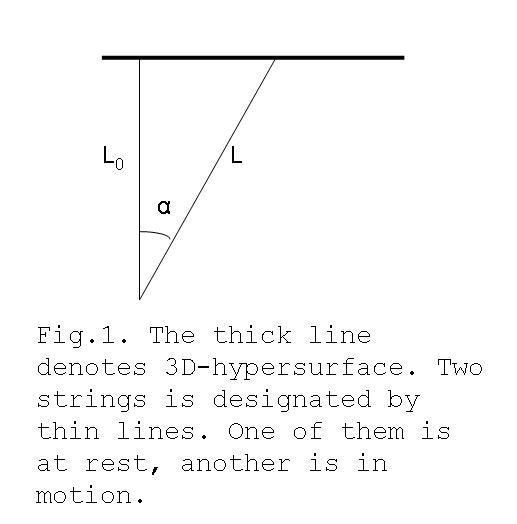Therefore, if to take into account that sin α = V/c, one may identify m and L, the mass of particle-string and the length of the string-particle into the additional fourth dimension. When we are considering some body, its mass due to the mass additivity property adds in from the separate masses, or lengths, of all particles from which the body consists. However, at small distances between the strings it is emerged the interactions which violate the additivity of the string lengths and lead to the mass defect.

Under that identification the mass dimensionality such as grams changes into the length dimensionality such as metres. Thereafter other dimensionality could be determined. For example, the force will have the dimensionality of the square of the velocity.

The same velocity dependance will be for the string energy if to adopt that the whole energy is kinetic. Then it can be bound with the medium (or "aether") motion around and along the string axis in such a manner as it might be for the vortex that the string is modeled for. It is obvious that the string kinetic energy E will be proportional to the string length if also to suppose that the distribution of the mean velocity of the medium would be uniform along the string axis if to level the velocity up along the string cross section. It will be so if the square of the averaged velocity of the string unit length would be constant. Denoting it by c² we go to the famous expression

E = mc².

(3)

The one-demensional string model is certainly not fit to describe the medium points' movement with the velocities close to the speed of light c. Moreover, it is quite hard to imagine a whirling movement because it occurs around two-dimensional plane in 4D space. We will consider it elsewhere. Here we are to point out that there is a void cavity along the axis of the real vortex and it must be a force to balance the centrifugal force with which the medium aims to run away from the void during its rotation. The surface tension force is such one and it is equal to σK, where K is the mean curvature and σ is a coefficient of the surface (or "hypersurface") tension. For simplicity we take the vortex has the cylindrical symmetry. The cross section of its cavity is a sphere. If its radius is a, the medium particles forming the cavity wall are in equilibrium, i.e. on the Bernoulli surface of the flow, it is need the minimum value will be gained for the next expression

u_s²/2 + 2σ/a.

(4)

σ is declared here as refered to the unit of the mass (or to the unit of the vortex length), u_s is the rotation velocity which we represent as aω with ω to be the angular velocity. Finding the minimun of the expression (4) we get

a³ = 2σ/ω².

(5)

We see that the size of the vortex can not be arbitrary and that the relationship of the vortex radius with the rotation period T = 2π/ω is the same as in the second Kepler's law. The velocity of the vortex wall being found from the eq.(5)

u_s = aω = √(2σ/a).

(6)

is diverged at a = 0. That is why the suggestion about the existence of the minimun a which corresponds velocity maximun is made.

To count the kinetic energy of the vortex it is necessary to know the distribution function of the velocity of all meduim particles in the whole space. We take the following simple dependence for the absolute velocity value as a such distribution

u = u₀ exp -a/μ.

(7)

Here μ is a damping parameter of the velocity having the length dimensionality and u₀ is a some virtual velocity at the center of the vortex cavity where a = 0. The real velocity of the vortex wall u_s can be determine under substitution r = a into eq.(6). Comparing two last expressions one can find a from the following equation

u₀ exp -a/μ = √(2σ/a).

(8)

By integrating half of the square of u through the whole space except the cavity we find the quantity that one can name as the vortex energy.

E = 4πμLu₀²exp -2a/μ(a² + aμ + μ²/2)

(9)

It was suggested here the uniformity of the velocity distribution along the vortex axis. To avoid this supposion, which is obviously not true in the vicinity of the hypersurface, one can use an effective value of the vortex length and understand the mean velocity under u₀ in eq.(7). Using eq.(8) the vortex energy can be represented in the following form

E = 8σπμL(a + μ + μ²/2a)

(10)

Varying it on a, one can find the minimun energy value

E = 16σπa²L(1 + √2),

(11)

which achieves at

a = μ/√2.

(12)

Finally we get eq.(3) if to denote

�² = 2σ/a

(13)

and

m = 4πa³L(1 + √2).

(14)

So the mass is proportional to L and has a quantity 4πa³(1 + √2) as a coefficient of the proportionalty, which is equal to 3D-volume of the cross-section 4πa³/3 multiplied on 3(1 + √2) = 7,2426. One can say that with a account of this numeric coefficient the mass is a 4D-volume of the vortex cavity. But due to the constancy of the radius a this volume depends only on L, at least for small deviations of the vortex axis from the hypersurface normal. In the latter case one can expect another form for the dependancy (1).

The condition (13) means that v_s is equal as it was said above to maximun value of the velocity, i.e. the speed of light, which is correspondent to minimun value of the vortex cavity radius. The vortices with bigger size also can exist but they are not stable. The stable particle such as the electron can therefore pretend on the role of the real particle with the property described above.

Therefore the supposition about the particle mass and its length proportionality is quite validated and the model of 4D-medium, in some degree, let us to come near to the resolve of the task posed by John Wheeler to lead the physics to the geometry.

[1] V.Skorobogatov. The light in 4D-aether model.2006. http://vps137.narod.ru/article2a.html.