Системы отсчета в 4D-модели эфира

В. Скоробогатов

Было показано [1], что нулевой результат опыта Майкельсона-Морли можно было бы объяснить с помощью модели 4D-среды ("эфира"), допустив существование скоростей света как больше, так и меньше стандартного значения c. Такие скорости могли бы зависеть от скорости зеркала V, от которого отражается свет. В противном случае, когда скорость света предполагается постоянной, расхождение в путях света в продольном и поперечном направлениях достигает второй степени V/c, где V - скорость эфира относительно поверхности Земли, где, как предполагается проводится опыт.
Здесь мы обсудим выбор систем отсчета в модели и затронем вопрос о так называемом замедлении времени, который является одним из самых дебатируемых в теории относительности.

Кроме того, применение галилеевых преобразований, использовавшихся при трактовке результата опыта Майкельсона-Морли, требует большего обоснования для использования в той форме, которая была предложена.

Вначале рассмотрим две системы отсчета в 3D пространстве, K и K'. Одна из них покоится, а другая движется с постоянной скоростью V. Обычно соответствующие оси координат этих систем выбираются параллельными друг другу. Тогда, если скорость направлена вдоль оси x, преобразование Галилея записывается в виде

x' = x - Vt.

(1)

Есть простое взаимное соотношение, или симметрия, между обеими системами при их взаимозамене (т.е. когда K' считается неподвижной и скорость системы K измеряется относительно ее):

x = x' + Vt.

(2)

Мы видим, что только знак у скорости V изменился, когда системы поменялись местами. Время t не изменяется при этих преобразованиях.
Требование коллинеарности осей не является строгим. Можно выбрать любую ориентацию для системы отсчета. Например, если движущаяся система K' повернута вокруг третьей оси на угол α относительно соответствующей оси системы K, то соотношение (1) изменится на следующее:

x' = (x - Vt) cos(α).

(3)

Надо заметить, что так как операции вращения и трансляции не являются перестановочными, важен порядок этих операций. Здесь перемещение предшествует повороту.
Такое преобразование не дает ничего нового в рассмотрении движения, если только не принимать во внимание нарушение симметрии между системами:

x = x'/ cos(α) + Vt

(4)

При этом, конечно, различие в форме последних двух выражений не означает, что взаимная скорость движения систем изменилась. Надо учесть изменение второй координаты, так как направление скорости в системе K' изменилось. В общем случае ур.(3) может быть записано в виде

r' = M (r - Vt)

(5)

где M - ортогональная матрица, описывающая вращение. Обратное преобразование будет выглядеть как

r = M*r' + Vt,

(6)

Мы видим, что скорость V в одной системе превращается в MV в другой системе, когда эта система повернута на угол α.
В таком рассмотрении неявно предполагается, что обе системы могут быть связаны с телами. В классической физике наилучшим приближением к физическому телу является материальная точка, но это не так в 4D-модели эфира. Здесь таким приближением, также как и моделью отдельной частицы, является двумерный объект, струна или линия, пересекающая границу эфира, точнее, имеющая точку касания с ней. Отсюда следует, что 4D-система отсчета должна соответствовать положению движущегося тела, т.е. положению струны. Как показано [1], телу, находящемуся в покое, соответствует линия, перпендикулярно расположенная к границе среды, а движению тела - наклон этой линии. Поэтому нам надо повернуть движущуюся систему отсчета, если мы хотим, чтобы она была связана с движущимся телом. Угол поворота должен быть таким же, как угол отклонения линии от нормального положения. Тогда если наблюдателю придать импульс в направлении движения, то ему будет казаться, что тела, движущиеся вместе с ним с той же скоростью, находятся как бы в покое.

Мы можем описать такой поворот в 4D пространстве с помощью матрицы

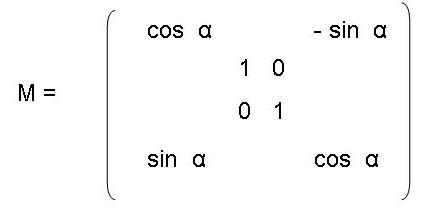(7)

Здесь предполагается, что r - 4-х мерный радиус-вектор. Следует заметить, что в 4-х мерном пространстве вращение происходит не вокруг какой-то одной оси, а вокруг двух осей, или вокруг двумерной плоскости, натянутой на эти оси. Используя эту матрицу в ур.(6) легко получить

x = x'cos(α) - z' sin(α) + Vt
z = x'sin(α) + z' cos(α)

(8)

где z означает четвертую координату точки в 4D среде. Выберем границу так, чтобы она описывалась с помощью выражения

z = 0.

(9)

Тогда если исключить z' из (8), мы получим из первого уравнения в точности ур.(4). После этого, если принять во внимание, что в соответствии с [1]

V = c sin α,

(10)

ур.(4) можно представить как

x' = (x - Vt)/√(1-(V/c)²)

(11)

Это ничто иное, как преобразование Лоренца для пространственной координаты.
Подставив (10) в первое уравнение (8) мы получим

x = x'cos(α) - (z'- ct) sin(α)

(12)

Оно выглядит как первая часть ортогонального преобразования. Можно формально построить вторую часть

z - ct' = x'sin(α) + (z'- ct) cos(α)

(13)

Есл подставить сюда z из второго уравнения (8), то нетрудно получить следующее выражение

t' = t cos(α)

(14)

С другой стороны, если положить

z = z' = 0

(15)

и использовать определение скорости с помощью ур.(10), то получится преобразование Лоренца для времени:

t = (x'V/c² + t')/√(1-(V/c)²)

(16)

Чтобы получить взаимное преобразование нужно подставить это выражение в ур.(11) и сделать некоторые упрощения:

t' = (-xV/c² + t)/√(1-(V/c)²)

(17)

Обсуждение

Чтобы лучше представить себе смысл выражений, полученных выше, рассмотрим рис.1, на котором представлена ситуация с двумя системами отсчета так, как и в работе [1]. Здесь ось y представляет любое направление в плоскости, образованной второй и третьей осями. Вместе с осью x эта плоскость образует трехмерное пространство, или "мир", соответствующий ур.(9). Оно представлено на рис.1 в виде горизонтальной плоскости. Две другие плоскости, которые пересекают ее, представляют положение движущейся системы отсчета в начальный момент времени и в момент t. Они имеют наклон по отношению к "миру" такой, что их четвертая ось z' шла вдоль движущегося тела, положение которого в данном случае совпадает с положением подвижного наблюдателя. Последний обозначен точечной линией.

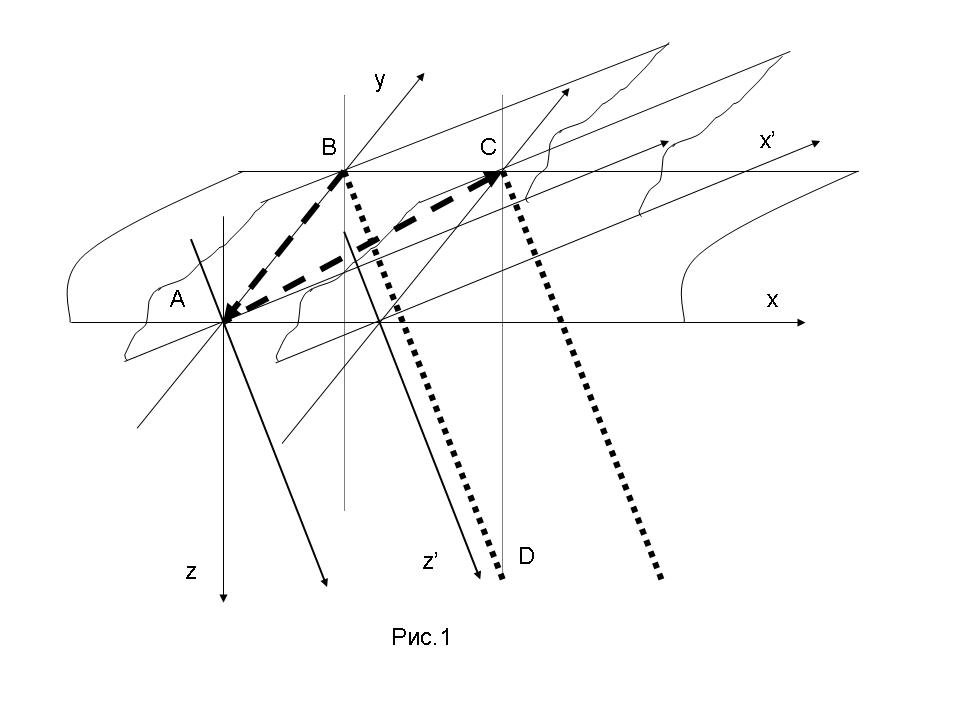Представим себе, что из начала покоящейся системы отсчета, отмеченного буквой A, также как из начала движущейся системы, отмеченного буквой B, одновременно испускаются пучки света, показанные пунктирными линиями. Так как свет может по предположению распространяться только внутри "мира" с постоянной скоростью c, то легко получить ур.(14). Расстояние ct' представляет собой путь, проходимый светом от точки A до точки C, куда сместится начало движущейся системы. Поэтому время t' есть время, нужное свету, чтобы пройти это расстояние в обеих системах. Но в отличии от покоящегося наблюдателя, находящегося в точке A, наблюдатель, движущийся из точки B в точку C, не может заметить, что свет проходит за пределами его координатной системы. Действительно, отрезок AC не содержится в системе отсчета, а лишь пересекает ее. Движущемуся наблюдателю может показаться, что свет распространяется от удаляющегося от него (по отношению к его местоположению в обратном направлении) наблюдателю в точке A, и он может заключить, что его время (т.е. время, нужное световому сигналу для того, чтобы пройти расстояние от него до другого наблюдателя) замедлилось. Но это не так, если посмотреть на всю картину в четырех измерениях. Мы понимаем, что свет идет в движущейся системе только вдоль взаимного пересечения двух координатный систем, т.е. вдоль двумерной плоскости, нормально расположенной к вектору скорости. Движущийся наблюдатель не способен воспринимать путь света BA целиком, потому что он уходит из этой плоскости во время движения.

Поэтому мы можем говорить о задержке времени только условно, также как и о сокращении длин. Отрезок BC также не содержится в движущейся системе, а лишь пересекает его. Из движущейся системы наблюдатель воспринимает проекции действительных расстояний, принадлежащих "миру". Формулы преобразования Лоренца справедливы при выполнении условия (15), которое соответствует плоскости взаимного пересечения и не могут распространяться на всю систему отсчета. При этом существенно, что первая формула (11) получена из преобразования Галилея (8) для двух координатных систем, повернутых по отношению друг к другу. Вторая формула (17) также возникает из преобразования Галилея, но при дополнительном требовании (15), ограничивающее область общего для обеих систем отсчета пространства.

Намек на другую интерпретацию содержится в ур.(12,13). Выражение z - ct выгладит как аргумент некой волновой функции f. Для нее будет справедливым написать волновое уравнение

∂_t²f - c²∂_zf = 0

Тогда мы можем представить себе две волны, движущиеся со скоростью света вдоль осей z и z'. Первая из них соответствует телу в точке A, или неподвижному наблюдателю, вторая - движущемуся телу. Значение z'- ct, деленное на длину волны, соответствует постоянной фазе с точки зрения неподвижного наблюдателя. Соотношения (12,13) поэтому имеют отношение к изменению фазы волны во время движения.

Это может помочь нам описать процесс эмиссии света следующим образом. Волна, существующая в некотором атоме (в четвертом измерении), достигает поверхности, границы среды или "мира", и производит на ней возмущение. Так как фаза "внутренней" волны в момент, когда волна выходит на поверхность ("гиперповерхность"), произвольна, то "внешняя" волна испускается в произвольном направлении. Эта внешняя волна, (видимый свет, если, конечно, длина волны соответствующая!), имеет те же параметры, что и внутренняя. Т.е. она движется по границе с той же скоростью и имеет ту же длину волны. Если она наталкивается на другой атом со схожими параметрами, она поглащается этим атомом, его электронами. Такое рассмотрение оправдывает высказывание, сделанное в работе [1] о том, что фотон - это часть электрона.

При рассмотрении систем отсчета в теории относительности всегда предполагалось их параллельное расположение. Поэтому происходит изменение длин и времен при попытке согласовать возникающий наклон движущейся системы отсчета по отношению к непожвижной. Говоря другими словами, движущийся наблюдатель живет в "воображаемом мире", который имеет лишь плоскость, перпендикулярную вектору скорости, в качестве общей части пространства с наблюдателем, находящемся в покое. Его мир призведен скользящим поворотом и его оценки расстояний и времен в нем неправильны. Это не значит, что теория относительности не верна. Она "работает", но не дает реальной картины для 4D-модели эфира. Чтобы давать правдоподобные результаты в ней вводится искусственное 4D пространство-время. В данной работе показано, как можно иначе их интерпретировать в реальном геометрическом пространстве.

Дополнение. О понятиях СТО.

Дополнение 2. Сложение скоростей.

[1] В.Скоробогатов. Свет в модели 4D эфира. http://vps137.narod.ru/phys/article2.html. 2006.